Python機械学習アルゴリズム学習備忘録。今回は強化学習 – Thompson Sampling – について。
内容は、Udemy ![]() の「【世界で74万人が受講】基礎から理解し、Pythonで実装!機械学習26のアルゴリズムを理論と実践を通じてマスターしよう」で学んだ内容を自分用備忘録としてまとめたものです。
の「【世界で74万人が受講】基礎から理解し、Pythonで実装!機械学習26のアルゴリズムを理論と実践を通じてマスターしよう」で学んだ内容を自分用備忘録としてまとめたものです。
参考:みんなのAI講座 ゼロからPythonで学ぶ人工知能と機械学習
Thompson Samplingとは -具体例と直感的な理解-
Thompson Samplinについて、具体例を使って直感的に理解するところから。
ランチでどのお店の行くかを考える。候補のお店が3つあり、3つのお店はいずれも初めていくお店で事前情報はなし。
3つのお店それぞれに、数日かけて各4回ずつ行ったとする。このとき、各お店で4回それぞれの満足度とその確率をグラフにしていく。
3つのお店それぞれの満足度の最頻値が、4回ずつ行った時点での各お店の想定満足度=次回行った際に得られる確率が最も高い満足度の値、となる。
この状態で、各お店に5回目に訪れた際、4回ずつ行った時点で算出された想定満足度に対して、5回目の満足度が高いか低いかに応じて、満足度と確率のグラフの高さと幅を調整する。
これを何度か繰り返していくと、満足度と確率のグラフは、一定の値の近辺に収束していく。つまり、最も確率の高い満足度の値に収束していく。
イメージとしてはこんな感じ。

“Reinforcement Learning: Thompson Sampling to Solve The Multi-Armed Bandit Problem-Part 1“
事前情報なしの最初の段階では、どのお店も同じような形の確率分布。
“Reinforcement Learning: Thompson Sampling to Solve The Multi-Armed Bandit Problem-Part 1”
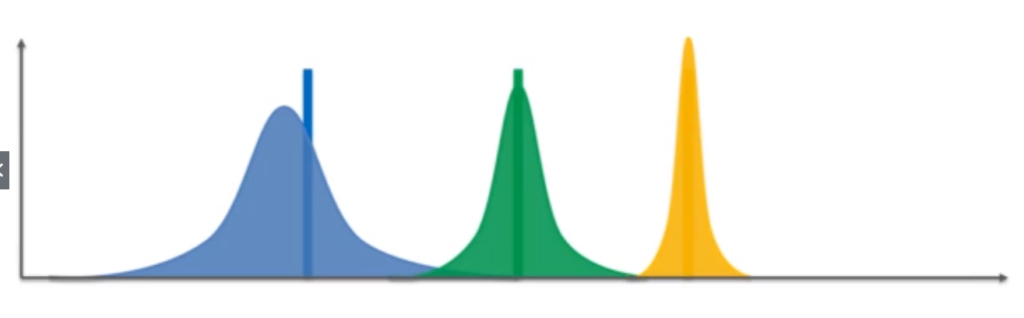
それが、試行回数を重ねていくと、得られた満足度とその確率に応じてグラフが変形し、収束していく。
例えば、上の図で、青のグラフも緑のグラフも、黄色のグラフと同じような形まで収束した場合、確率分布から、黄色のグラフのお店が最も高い満足度を得られる確率が高いお店で、緑がその次、青が得られるであろう満足度が最も低いお店である、と判断することができる。
このようにランダムなサンプリングと確率による手法がThompson Samplingである。
目次に戻るThompson Samplingとは -UCBとの比較-
上記の例では、まだ少しイメージが湧きにくい気がするので、強化学習のもう一つの手法である、Upper Confidence Bound (UCB)との比較を加えてみようと思う。
Upper Confidence Bound(UCB)については、こちらも。
【機械学習アルゴリズム学習備忘録】強化学習 – Upper Confidence Bound (UCB) –
Upper Confidence Bound
- 確率的ではない
- 値をすぐに反映する必要がある。
Thompson Sampling
- 確率的である。⇛それぞれのデータにおける確率に基づいて最も適切なデータを絞り込んでいく。
- 値の反映は後でも良い。⇛あくまで確率的にアルゴリズムが働くので、値の更新を都度行う必要はない。
- 論文などの情報が多い。有益なアルゴリズムであることが述べられていることも多い。
このUCBとThompson Samplingの比較にも具体例を使ってみようと思う。
ラーメン屋に行く場合で考えてみる。
A, B, C、3つのラーメン屋があるとする。
このとき、UCBの場合は、Aのラーメン屋に行った後、Aの満足度を一度記録し、毎回各お店について採点をしていく。その情報を踏まえた上で、次に行くラーメン屋を、「活用」と「探索」を用いて決定していく。
それぞれのお店に行くごとに満足度の情報を更新していくので、最終的に最も高い点数を得られたお店に行く頻度が高くなっていく。
一方で、Thompson Samplingで考えると、例えば、全体で100回ラーメン屋にいく(=試行回数を100とする)場合、A, B, Cそれぞれのお店に行っても、満足度などの情報は毎回細かく更新しない。
n回行った後、そのn回のうちに最も頻度の高かった満足度をベースに、それぞれのお店に行くとどれぐらいの満足度が得られそうかをイメージして、次に行くお店を決めていく。
これを繰り返していくと、だんだん各お店に対する自分の中の印象が固まっていく。つまり、Aのお店に行けばこれぐらいの満足度が得られそうだな、Bだとこれぐらい、Cだとこれぐらい、という感じ。
少しThompson Samplingのイメージが固まってきたような…。
目次に戻るThompson Samplingの手順 -数式的に-
Thompson Samplingの手順について。広告の効果測定をベースに。
Step 1. それぞれのラウンドnにおいて、広告iに対して以下の数字を求める。
Ni1(n) : ラウンドnまでに広告iが報酬1を得た回数
Ni2(n) : ラウンドnまでに広告iが報酬0を得た回数
※UCBとの違いとして、Thompson Samplingの場合は報酬0の場合も記録していく。
Step 2. それぞれの広告iに関し、以下の式に基づいたランダムな数を得る。
θi(n) = β[Ni1(n) + 1, Ni0(n) + 1]
※ベータ関数/ベータ分布:報酬1と報酬0のそれぞれの場合の期待値の分布
参考:ベータ分布とは?誰でも理解できるようにわかりやすく解説
Step 3. θi(n)の値が最も大きい広告を選ぶ
Pythonによる実装
ここからPythonを使って、実装していく。
ライブラリのインポート
まずはいつも通り使用するライブラリをインポートしていく。
import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
import random # アルゴリズムの中でランダムに値を取っていくので、randomモジュールもimportしておく。データセットのインポート
次にデータセットをインポートする。
dataset = pd.read_csv('ファイル名.csv')Thompson Samplingの実装
上記で述べた手順に従って、Thompson Samplingのアルゴリズムを実装していく。
N = 1000 # ラウンドの数
d = 10 # データの数
ads_selected = [] # アルゴリズムで選択された広告の番号を入れるリスト
numbers_of_rewards_1 = [0] * d # 報酬1が得られた回数を入れるリスト
numbers_of_rewards_0 = [0] * d # 報酬0が得られた回数を入れるリスト
total_reward = 0
for n in range(0, N):
max_random = 0
ad = 0
for i in range(0, N): # 1-10までの広告を順番に入れていく
random_beta = random.betavariate(numbers_of_rewards_1[i] + 1, numbers_of_rewards_0[i] + 1)
# 手順のStep 3で出てきたθの値を出す式。
# 10個の広告それぞれの報酬の値を引数として入れる。+1としているのはテクニカルな理由。
if random_beta > max_random:
max_random = random_beta
ad = i
# θの値が最大のものを選択していく。
ads_selected.append(ad) # 選ばれた広告をリストに入れる。
reward = dataset.values[n, ad] # ラウンドごとに、選ばれた広告が実際にクリックされているかどうか。実際に得た報酬の値を変数rewardに入れている。
if reward == 1:
numbers_of_rewards_1[ad] = numbers_of_rewards_1[ad] + 1
else:
numbers_of_rewards_0[ad] = numbers_of_rewards_0[ad] + 1
total_reward = total_reward + reward
結果の可視化
最後にmatplotlibを使って、ヒストグラムの形で結果を可視化していく。
一気に最終結果だけ可視化してもいいし、ラウンド数を変えながら例えば、本来1000回ラウンドがあるとして、500回ぐらいにして途中経過を観察することも可能。
plt.hist(ads_selected)
plt.title('Histogram of ads selections')
plt.xlabel('Ads')
plt.ylabel('Number of times each ad was selected')
plt.show()まとめ
UCB、Thompson Samplingと2種類の強化学習手法についてまとめてきた。ここでまとめを書いておこうと思います。
強化学習とは:
報酬や罰則を与えることで機械に学習をさせていく手法。機械は、報酬を最大化させるように学習をしていく。例えば、将棋なんかの場合、機械が選択した手に対して、いい手であれば報酬を与える、ということをすると、機械は報酬を最大化するような手を算出し、より強い将棋を打つことができるようになっていく。
この強化学習の手法として、
の2種類の手法がある。
UCBは、試行のたびに期待値に関する情報と報酬を更新し、最終的に最も高い報酬を得たデータを最適解として選んでいく手法。
一方で、Thompson Samplingは、各データが、最も高い確率で得られる期待値・報酬を得られる確率を算出し、最も高い期待値・報酬を得られる確率が最も高いデータを最適解として選んでいく。
Thompson Samplingのほうが演算処理が軽く、精度も高いため、有益なアルゴリズムである、との意見も多い。
しかしながら、解決したい問題によってはUCBが適しているケースもあるので、一概にThompson Samplingのほうが必ずUCBよりも優れている、とは言えず、複数のアルゴリズムを試し、よりもっともらしい結果を返すアルゴリズムを採用していくのが良い。
というわけで、今回は強化学習のThompson Samplingについてのまとめをしてきました。
もし「ここの理解間違ってる」や「こういう考え方・使い方もできるよ」というのがありましたら、教えていただけますと幸いです。
では、最後まで読んでいただきありがとうございました。また次の記事で!




コメント